Temps de lecture : 10 minutes
Netmath a pour mission d’aider chaque élève à découvrir et développer son propre potentiel mathématique avec plaisir.
Simon, technopédagogue et expert Netmath, vous propose dans « Simon se demande » d’aborder avec vos élèves une question du quotidien d’un point de vue des mathématiques. Une façon pour eux de se rendre compte que les maths peuvent être vraiment le fun lorsqu’il s’agit de mieux comprendre le monde qui les entoure.
Aujourd’hui, parlons du choix cornélien du sapin de Noël!

Noël est un moment formidable dans l’année. Il s’agit d’une occasion de se rapprocher des gens qu’on aime pour profiter un peu de la douceur de l’hiver. Et dans cette atmosphère festive, le sapin joue très certainement un rôle central! Je me demande ici s’il est possible de faire un bon ou un mauvais choix de sapin. Et s’il y a une manière d’établir un critère pour déterminer sur le champ si notre choix fera l’unanimité.
Vous vous souvenez de Carl? Oui! Ça tombe bien parce que Carl adore la période des fêtes … surtout pour la décoration du sapin!

Il part donc en quête du sapin parfait, avec la bonne intention de ne pas décevoir ses proches une nouvelle fois cette année!

Après tout, cette décision a des répercussions considérables étant donné que ce sapin sera à la vue de tous pendant environ un mois! Sans compter toutes ses apparitions sur photos partagées sur les médias sociaux (mais c’est un autre sujet ;)). Bon. Comment aider Carl à choisir son sapin?
D’abord, on va vouloir comparer les sapins les uns aux autres. Et pour ce faire, on doit trouver un modèle qui pourra simplifier un peu la réflexion. En gros, ce modèle doit rendre la situation plus simple, mais encore réaliste! Je vous suggère donc de parler de sapins TRIANGULAIRES. Si vous n’êtes pas déjà convaincus de mon choix, peut-être que cet exemple rapide sera plus efficace 😉


Carl choisit son triangle sapin
Donc comme on disait, pour faire un choix, Carl doit comparer les sapins entre eux! Il prend la très bonne décision de considérer la hauteur et la largeur des sapins.
Par exemple, lorsque Carl observe ce sapin (appelons-le sapin 1), il prend en note une hauteur de 100 cm et une largeur de 200 cm.
Mais Carl réalise rapidement que ce n’est pas si simple de se fier à 2 valeurs (hauteur et largeur) pour chaque sapin. Il doit donc trouver une manière de simplifier l’information.
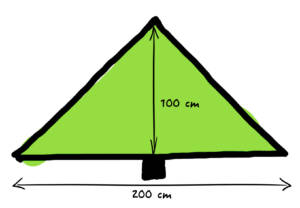
Soudain, idée de génie … déterminer le rapport entre la hauteur et la largeur. Pour conserver le même exemple, Carl fait le calcul suivant : (100 cm)/(200 cm) = 0,5. C’est la nouvelle étiquette qu’il donne à sapin 1.

Carl se met alors à l’oeuvre et il catégorise tous les sapins qu’il voit! Rapidement il réalise 2 choses :
- plusieurs sapins de tailles différentes peuvent avoir la même étiquette (rapport)
- certaines étiquettes sont TOUJOURS accolées à des sapins vraiment moins beaux
Prenons ces 2 découvertes une à la fois!
Plusieurs sapins ont la même étiquette
Revenons au cas de sapin 1. Son étiquette est 0,5 puisque c’est le rapport entre 100 cm (hauteur) et 200 cm (largeur). Mais quand on y pense, on pourrait imaginer un tout petit sapin d’une hauteur de 10 cm et pour respecter le rapport de 0,5 on pourrait imaginer que sa largeur est de 20 cm. Ce sapin aurait aussi une étiquette de 0,5.

J’arrive donc à la conclusion que chaque étiquette peut décrire une infinité de sapins! On crée en quelque sorte des familles de sapins semblables!
Ce qui reste inchangé, c’est l’allure des sapins de même famille. Effectivement, il y aura invariablement des familles constituées de moins beaux sapins 🙁
Les beaux … et les moins beaux sapins
Comme Carl l’a remarqué, on sait maintenant que chaque famille de sapins semblables contient une infinité de sapins. Et comme les sapins semblables ont la même allure, la comparaison des sapins revient en faite à comparer les familles!
Je me questionne : est-ce qu’il y a des proportions (étiquettes) plus prometteuses que d’autres! Selon vous, quel rapport sera associé aux plus beaux sapins? En d’autres mots, sur une droite numérique, où placeriez-vous l’étiquette “Beaux sapins” ?

À priori, j’aurais tendance à choisir un rapport près de la valeur du nombre d’or. Un nombre reconnu pour être associé à la beauté!
Le Nombre d’or, aussi connu sous le nom de divine proportion, se retrouve un peu partout dans la nature et selon certaines sources, ce nombre serait associé à la beauté. Cédric Villani par exemple est l’auteur d’un livre qui s’intitule Le nombre d’or, le langage mathématique de la beauté.
Mais rien n’est moins sûr! Une manière de vérifier cette hypothèse serait la suivante. Je vais vous présenter 4 sapins avec des rapports (hauteur / largeur) différentes. Les mesures de l’un de ces sapins respectent les proportions du nombres d’or. Pouvez-vous deviner lequel?

Si vous avez choisi le 2, vous avez opté pour le nombre d’or! Il faut dire que cette famille de sapins est effectivement assez jolie, mais je ne crois pas qu’à l’œil nu, nous puissions faire la distinction entre un rapport de 1,6, 1,5 ou même de 1,4.

Ce que je veux dire c’est qu’on peut voir une différence, mais il me semble difficile de dire que le rapport de 1,6 est vraiment plus joli que celui de 1,5 ou même que celui de 1,4. En d’autres mots, le nombre d’or n’est peut-être qu’un excellent représentant de l’ensemble des rapports dont les proportions sont plaisantes à regarder. Ça vaudra peut-être la peine de s’y attarder plus longuement dans un autre épisode 😉
Revenons à nos moutons sapins.
Il peut être intéressant de visualiser cette situation sous la forme d’un graphique. Effectivement, ici, chaque famille de sapins semblables se retrouvera sur la même droite. Les trapus, les élancés, les balancés … peu importe l’envergure, tous les sapins dont le rapport entre la hauteur et la largeur est la même seront alignés sur une même droite.

Finalement, Carl doit prendre une décision! D’abord, il identifie les régions du graphique qui correspondent à des sapins trop étroits ou trop trapus. En continuant ses éliminations, il arrive à déterminer sa famille préférée : les sapins ayants un rapport entre 1,5 et 1,7 entre la hauteur et la largeur de la base.
Carl vient donc de réduire considérablement l’éventail des possibilités parmi lesquelles il devra choisir! Mais il reste tout de même une infinité de sapins!
Effectivement, pour n’importe quelle hauteur, on peut trouver une largeur de sapin qui permettra de conserver une proportion de 1,6.

Heureusement pour lui, avant de partir, il a pris une mesure de la hauteur du plafond de son salon! Ça lui permettra de déterminer exactement, le sapin qu’il doit acheter. Comme son salon a une hauteur de 270 cm, il peut calculer la largeur du sapin parfait:

Voilà! Carl a finalement tout ce qu’il faut pour trouver le sapin parfait et vivre le meilleur temps des fêtes de l’histoire…
.

ou presque!
Activités connexes:
- S2 Trouver des mesures manquantes dans des situations de figures isométriques ou semblables: activité 1.
- S2 Résoudre des problèmes de géométrie à l’aide d’expressions algébriques: activité 2.
- S2 Utiliser le raisonnement proportionnel: activité 3 ou activité 4.
- Mission qui fait état du lien entre le nombre d’or et la suite de Fibonacci: activité 5.

