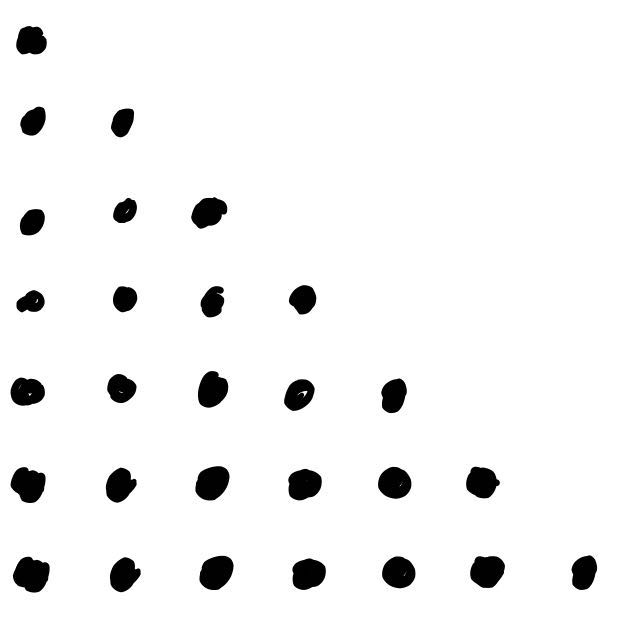Temps de lecture : 5 minutes

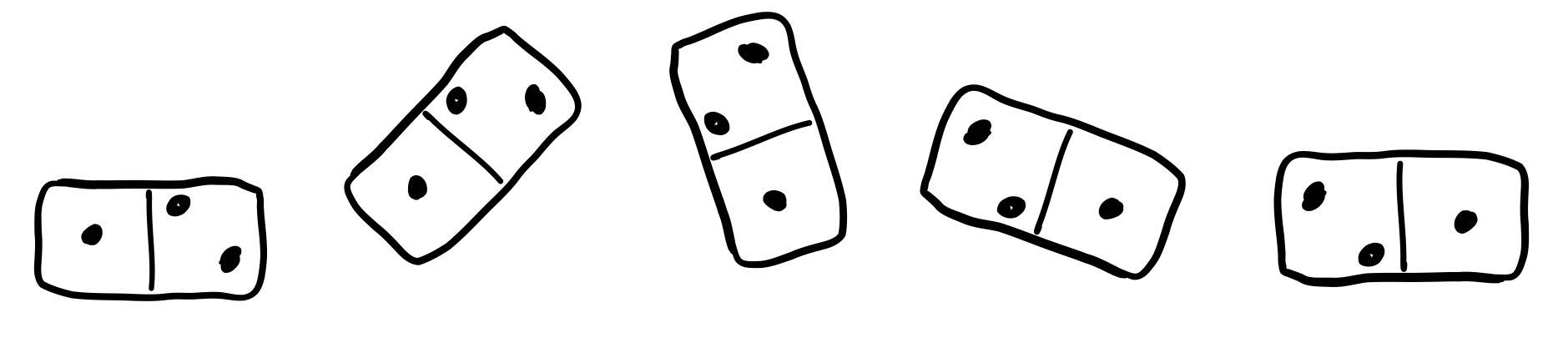
Je veux créer mon propre jeu de dominos!
La première question que je me pose, c’est: Combien de dominos je vais avoir à la fin?
Il y a une bonne différence entre se lancer dans un projet de 1000 morceaux ou de 10 morceaux. J’en suis où, là?
On doit partir du domino 0|0 jusqu’à 6|6.
Au fond, on peut probablement reconstituer tous les dominos en les reconstruisant. Je pourrais probablement organiser l’information dans un tableau.
Ah oui! Voilà :
Donc, si j’ai 7 possibilités pour le premier côté et 7 autres possibilités pour le 2e côté, il y aurait 7 x 7 = 49 dominos différents
Attends un peu. Quand on joue au domino, il n’y a qu’un exemplaire de chaque domino. 1|2 n’arrive qu’une seule fois. Pourtant, ici on a considéré 1|2 et 2|1 comme étant 2 dominos différents. Pourtant, c’est le même puisqu’on peut tourner le domino 1|2 pour obtenir 2|1.
Bon. C’est quoi l’impact de cette découverte incroyable (ah! ah! ah!) sur le nombre de dominos?
Wow, je viens de voir quelque chose dans le tableau!
Incroyable non? Toutes les version retournées des dominos se retrouvent de l’autre côté de la diagonale. Exactement comme si on avait fait appliqué une symétrie!
Ça veut donc dire que je dois considérer uniquement une des 2 versions de chaque domino.
Donc ici, je ne compte que les cas en vert.
En comptant ligne par ligne en partant d’en haut, j’ai :
1 domino + 2 dominos + 3 dominos + … + 7 dominos
Je vais appliquer une technique que j’ai apprise dans le livre The Math Olympian (Attention à l’anglais).
L’auteur appelait cette idée la méthode de l’escalier :
On commence en représentant chaque domino d’un seul ensemble (disons qu’un point représente un domino)
On cherche à compter le nombre total de dominos, alors voici l’idée: on ajoute un 2e ensemble et on l’ajoute à l’envers!
C’est alors beaucoup plus clair qu’il s’agit d’un rectangle de 7 points de large et 8 points de hauteur.
Comme on a représenté 2 ensembles de dominos, la moitié représentera 1 ensemble!

Ce qui est incroyable ici, c’est qu’on peut appliquer cette technique chaque fois qu’on additionne des nombres consécutifs!
En faisant l’exercice de dessiner tous les dominos une et une seule fois, je me rends compte qu’on en a effectivement 28!
Dernière question alors: supposons que je trouve un moyen de faire un point chaque 5 secondes, combien de temps sera nécessaire pour que je termine de tracer tous les points?
Pour ça, je vais avoir besoin de connaitre le nombre total de points dans un ensemble.
Sans explication, je vous laisse décrypter comment j’ai fait pour arriver au compte!
J’arrive donc à 2 x ( 21 + 27 + 30 ) + 12 = 168
Si je prends 5 secondes pour tracer chaque point, ça fera un total de
168 × 5 = 840 secondes, soit exactement 7 minutes
Il ne reste qu’à jouer maintenant!