Temps de lecture : 10 minutes

J’ai acheté un rouleau de papier d’emballage.
Je sais Caroline … ce n’est pas écologique.
Mais maintenant que c’est fait, maintenant que j’ai ce rouleau de papier entre les mains, qu’est-ce que je peux faire pour sauver la mise?

Effectivement Caroline, je pourrais le rapporter!
Mais juste avant, si tu le permets, j’aimerais réfléchir un peu pour savoir comment j’aurais pu faire pour emballer un maximum de cadeaux avec ce rouleau!
Bon, quelles sont les dimensions du rouleau que j’ai en ma possession.
D’abord, entendons-nous que ce n’est pas tant le rouleau que la surface couvrante qui est intéressante!
Je remarque que l’emballage me donne uniquement la mesure de l’aire de la surface: 12m2
Intéressant! Ça va m’aider très peu étant donné qu’il y a une infinité de combinaisons de longeur/largeur de papier dont l’aire est de 12m2.
Voici 2 exemples
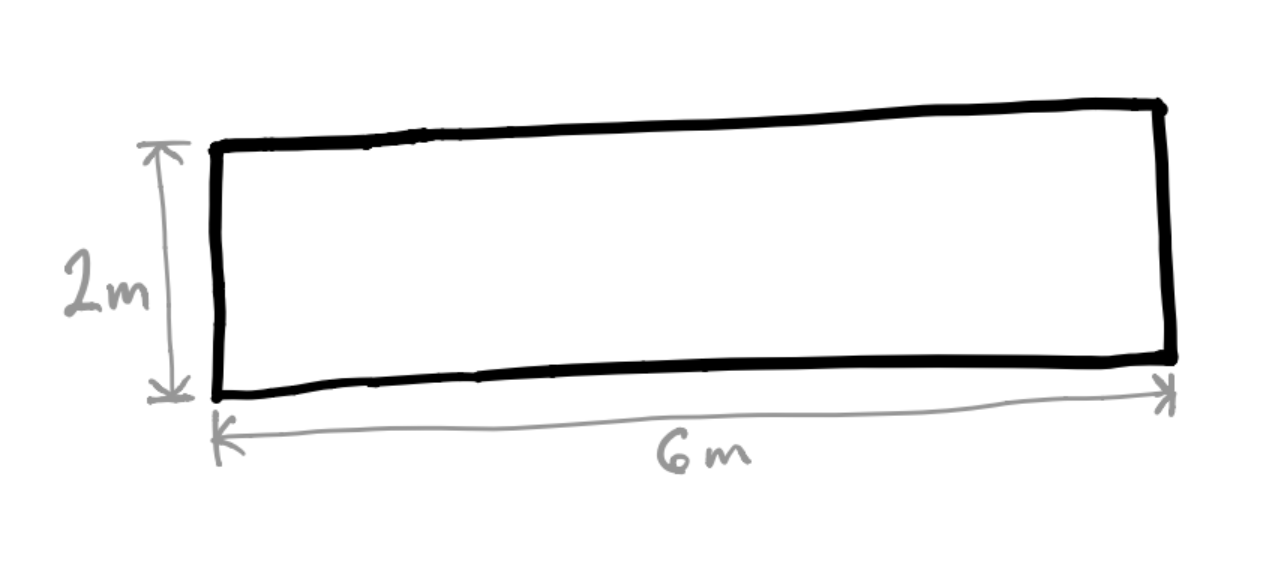
400
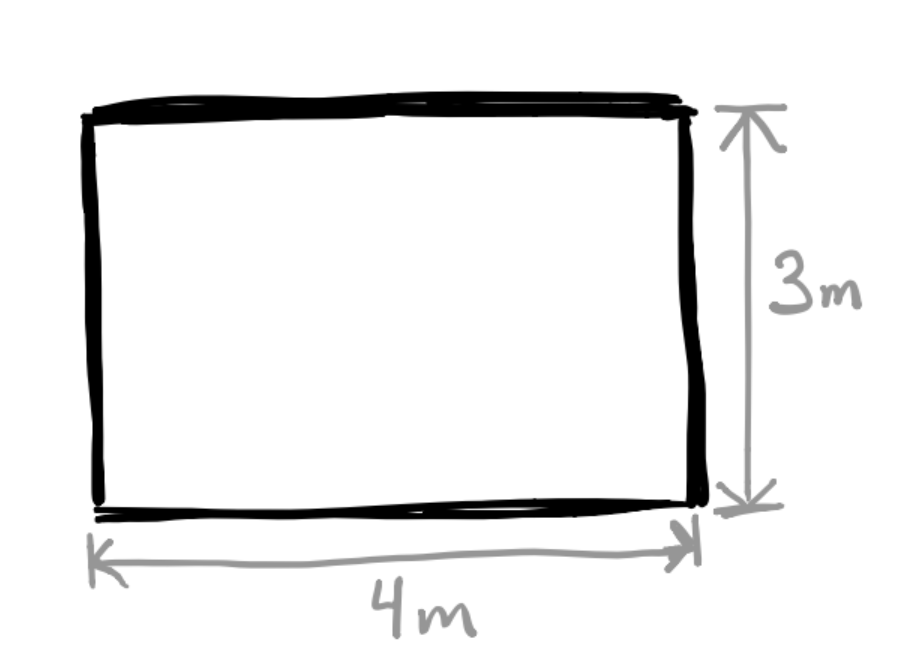
Je vais aller mesurer. Donnez-moi une minute et je reviens.
…
…
Ok je suis de retour!
La largeur du rouleau est d’environ 100 cm, donc la longueur est environ 12m.

Donc, au total, j’ai un papier de 12m de long et de 100 cm de largeur.
Bon!
Maintenant que je sais tout ça, comment je fais pour être le plus efficace possible pour emballer les cadeaux?
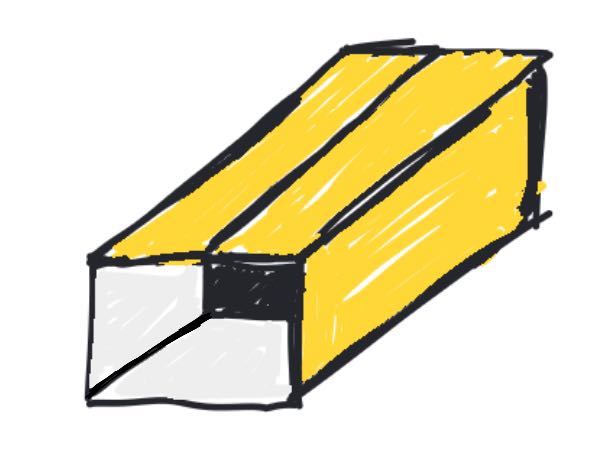
Premièrement, disons que j’ai un cadeau cubique à emballer. Et, pour simplifier le reste de la réflexion, disons aussi que la mesure d’un côté est de 1 unité (u).
Normalement, je procède de la manière la plus simple qu’il soit :
Grosso modo, j’essaie de faire en sorte que les 2 côtés du papier se rejoignent au centre de la face du dessus.
Voici un plan du cadeau disposé au centre du papier d’emballage :
Verticalement, je veux que les 2 côtés du papier se rejoignent sur le dessus de la boite, donc j’ai besoin d’environ 4 fois la longueur de la boite.
Horizontalement, je garde environ 3 fois la largeur de la boite pour que les rabats couvrent les côtés.
Je sais que ce n’est pas optimal, mais j’essaie de reproduire le cas classique de l’emballeur de cadeau moyennement expérimenté (moi).
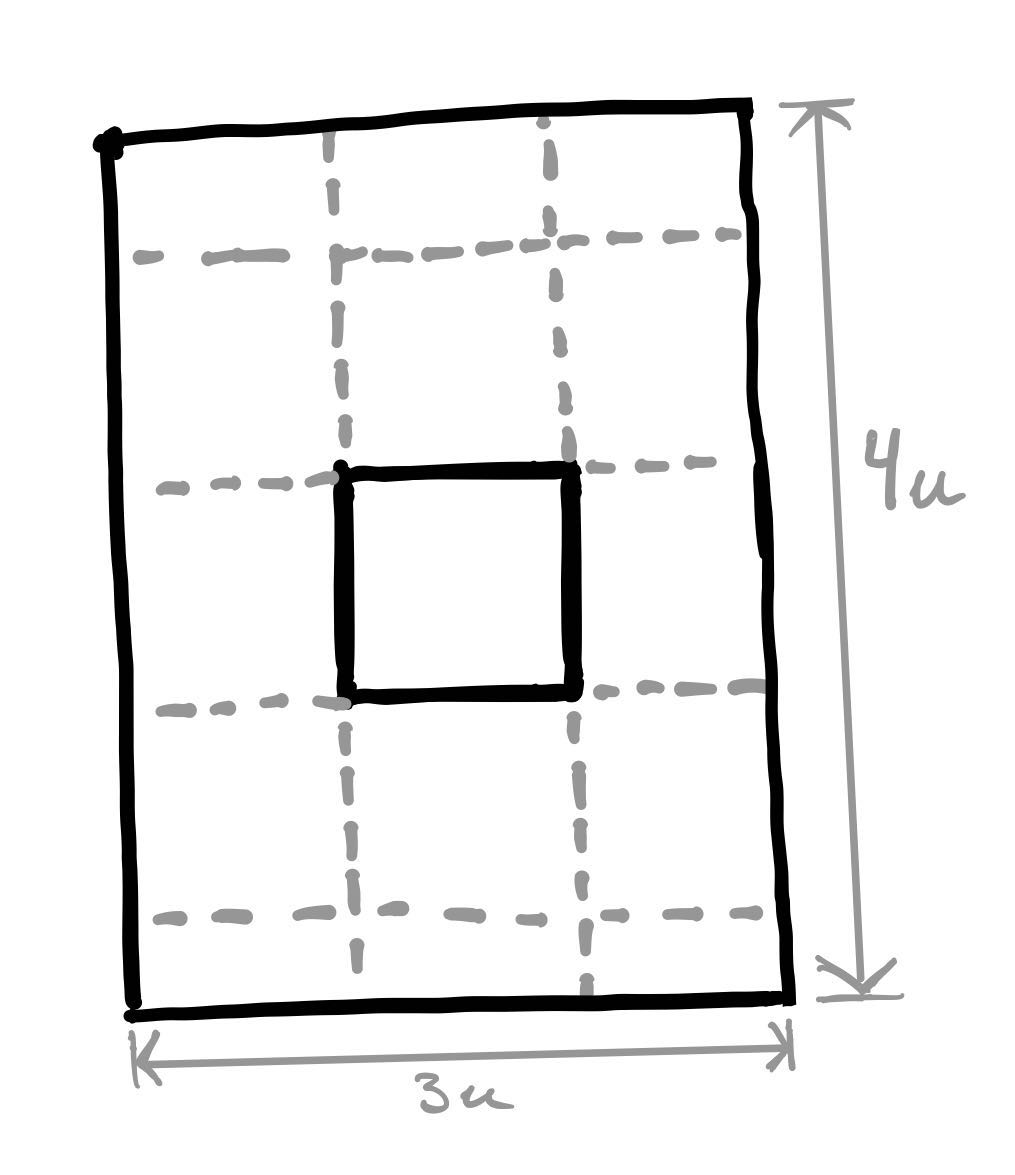
Pour résumer, j’ai utilisé une surface de 3x4 = 12u2 pour couvrir le cadeau.
Sur ces 12u2, la surface de la boite cubique représente 6u2.
On a donc 6u2 perdues. Cette surface de papier ne sert pas à recouvrir le cube.
Non Caroline, ce n’est pas très bon, ça.
Bon, comment on pourrait faire pour améliorer la situation?
Oh! Je pense avoir une idée!
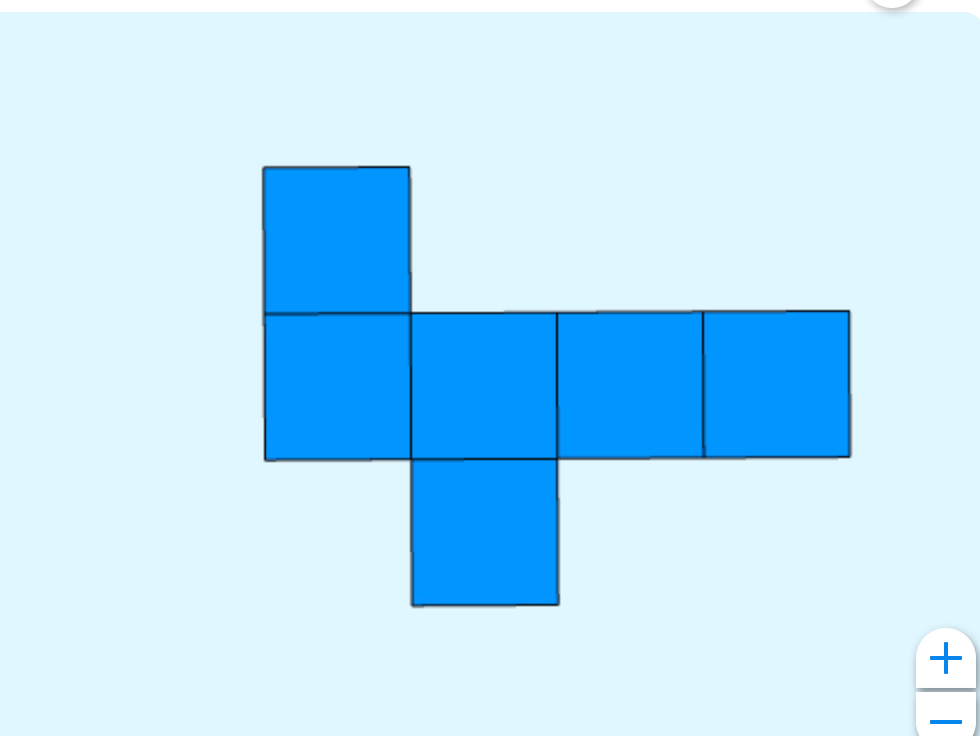
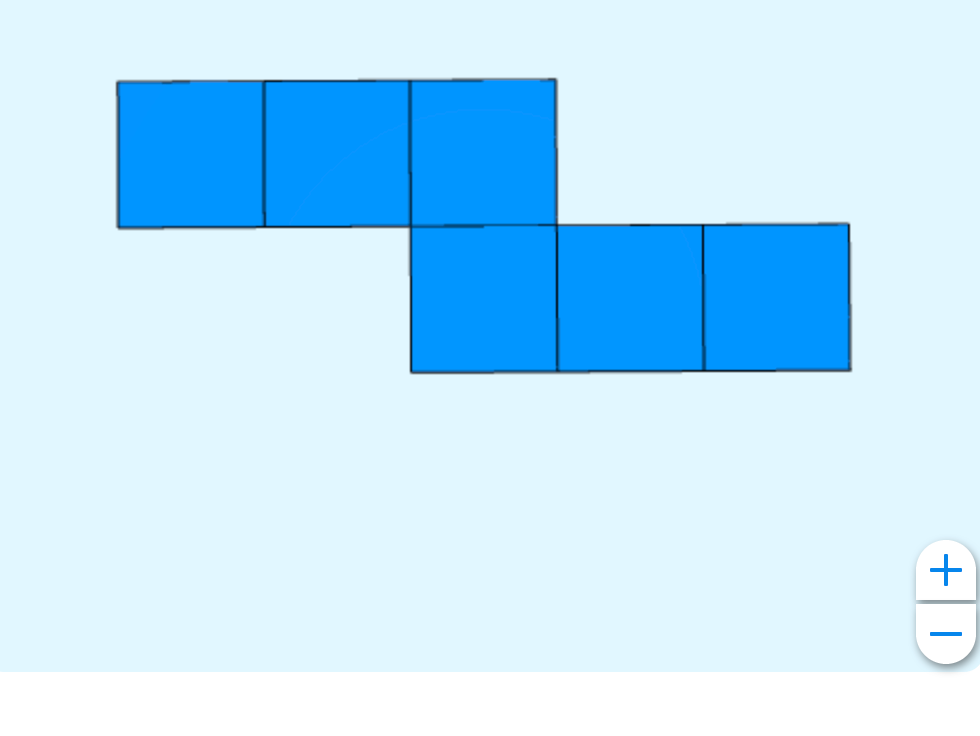
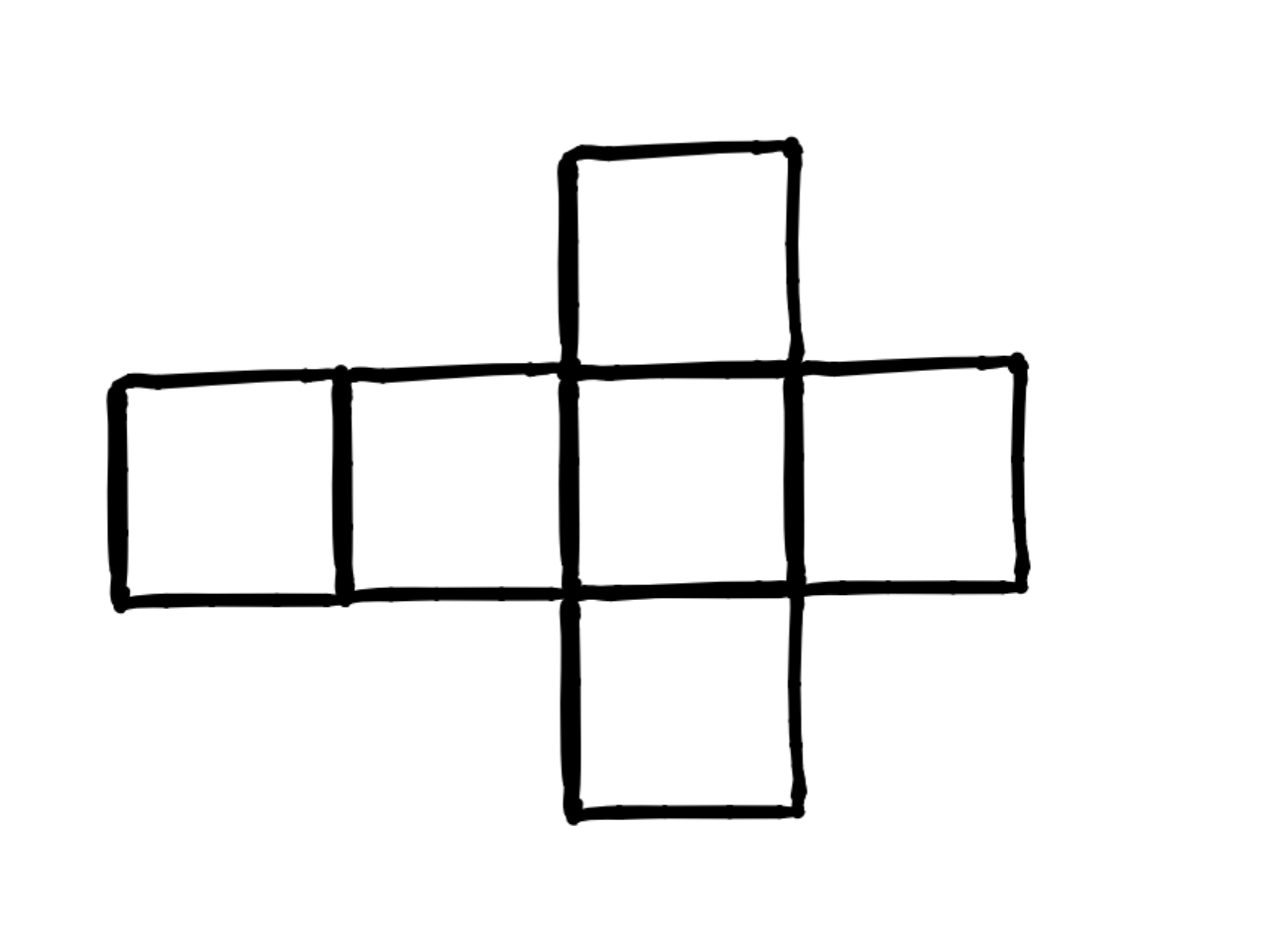
Imaginez qu’on se fie au développement du cube.
Mieux encore, je viens de penser que je peux utiliser l’outil de Netmath pour le représenter!

Notons que le développement que j’ai choisi ici n’est qu’une possibilité parmis plusieurs!
D’ailleurs, combien existe-t-il de développements du cube?
Si on découpait notre papier pour qu’il corresponde exactement au développement du cube, on aurait 0 perte.
Z.É. R. O.
Le rapport serait alors de 1:1. Chaque centimètre carré de papier servirait à couvrir une face du cadeau.
C’est incroyable!
Par contre, c’est loin d’être pratique parce que …
- … ça prendrait beaucoup de papier collant pour joindre toutes les faces
- … dès qu’une coupe est croche, ça engendre un trou par lequel on voit le cadeau
- … il y aurait probablement plein de retailles non utilisées
- … c’est long
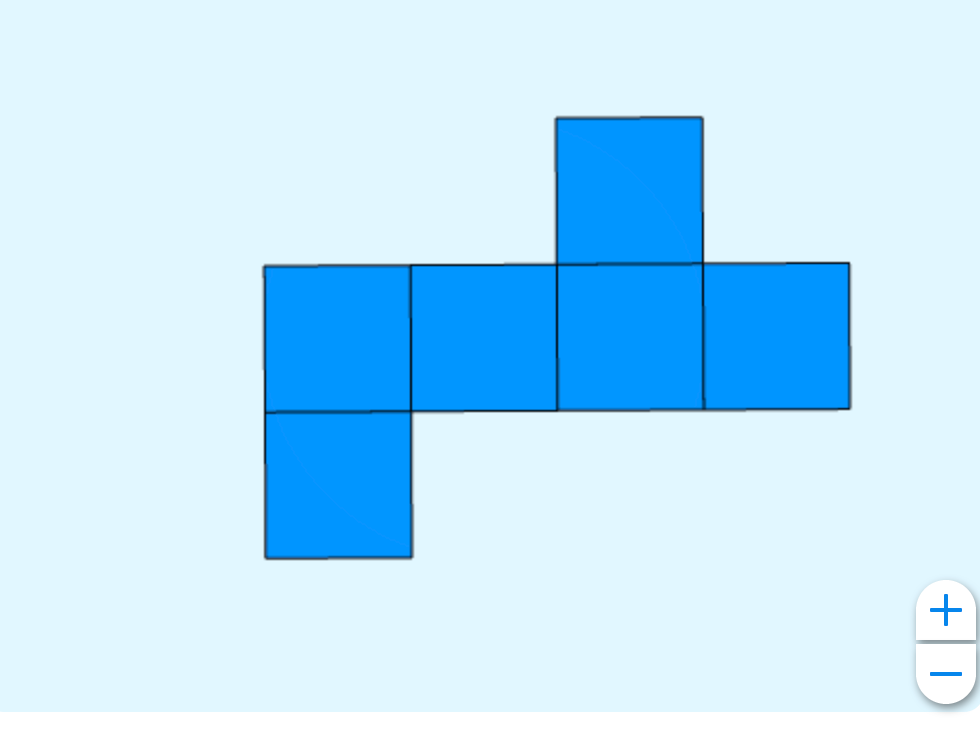
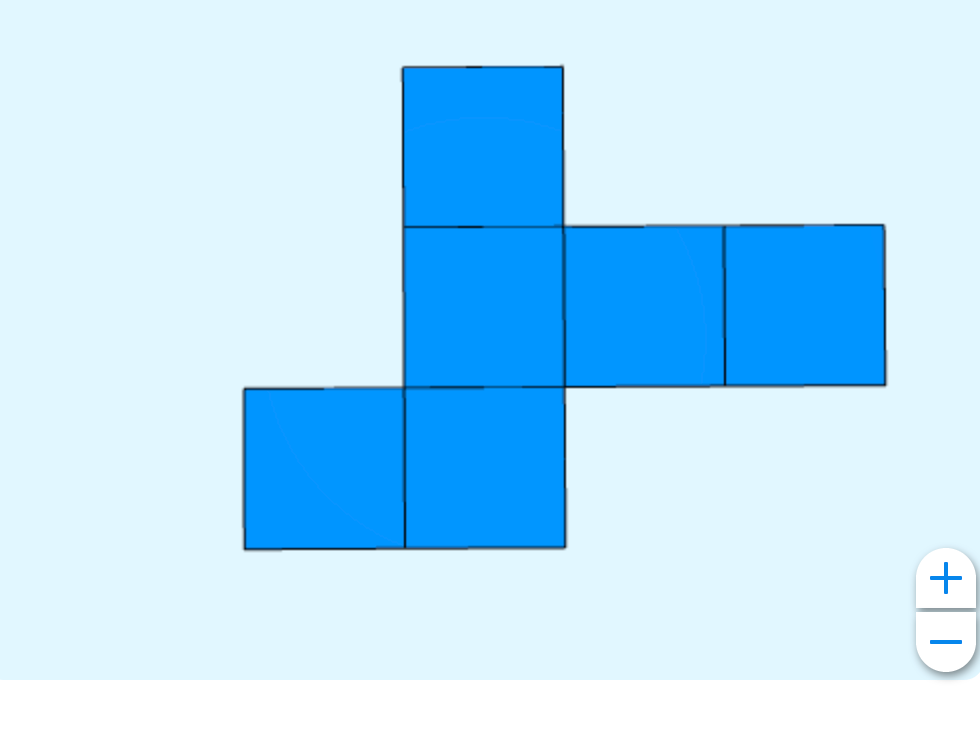
Mais partons quand même de ce développement :
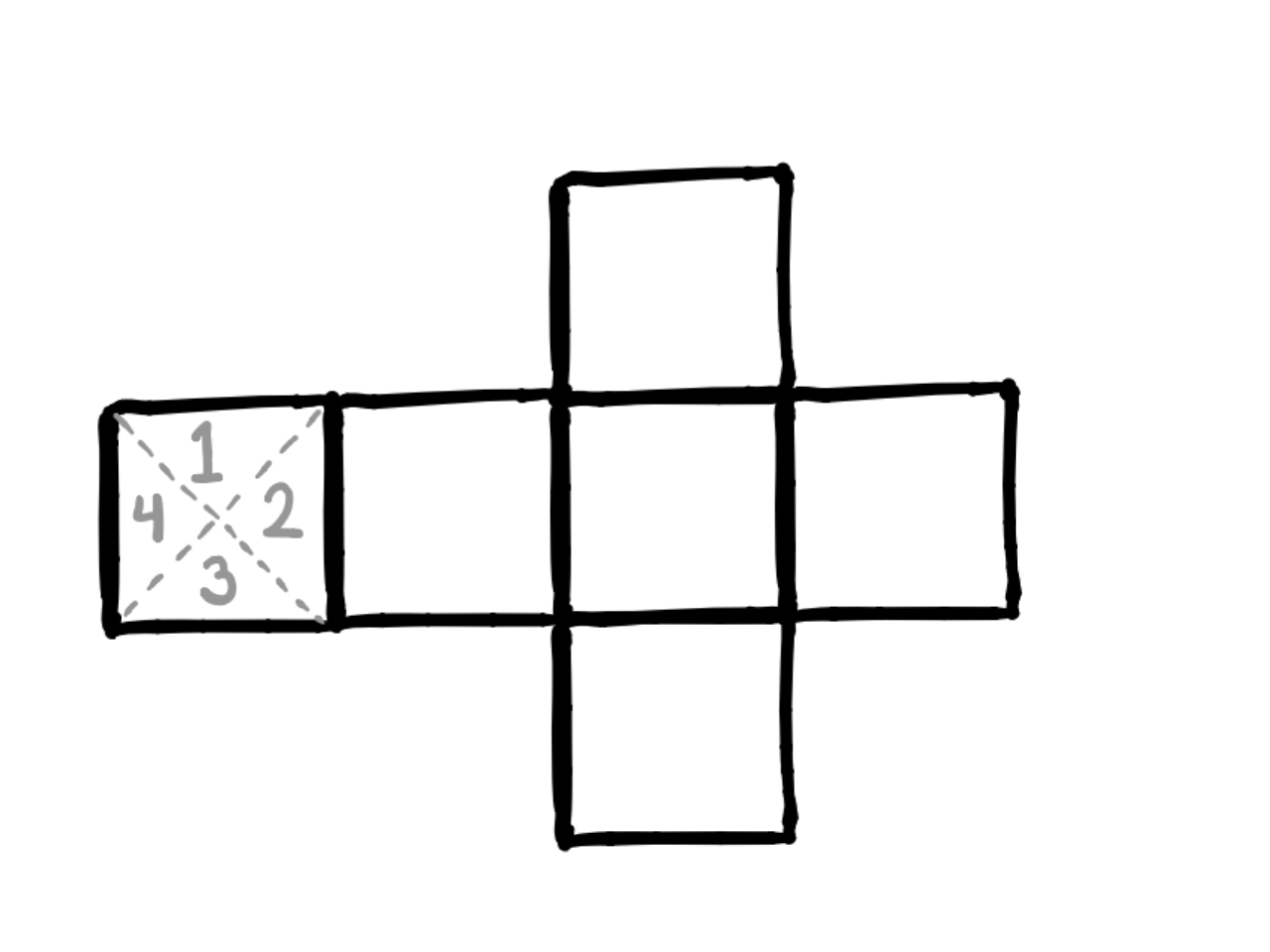
Voici mon idée!
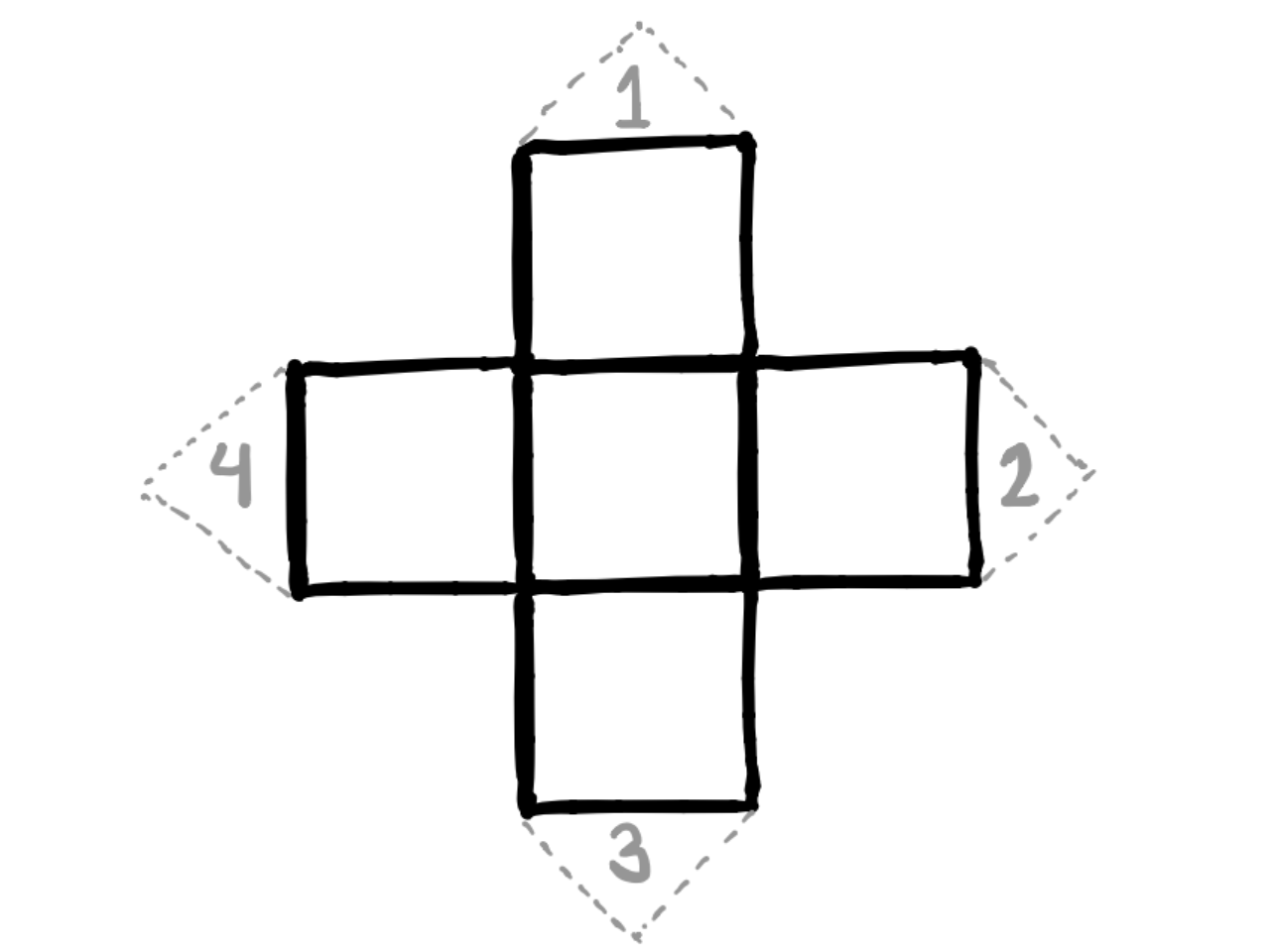
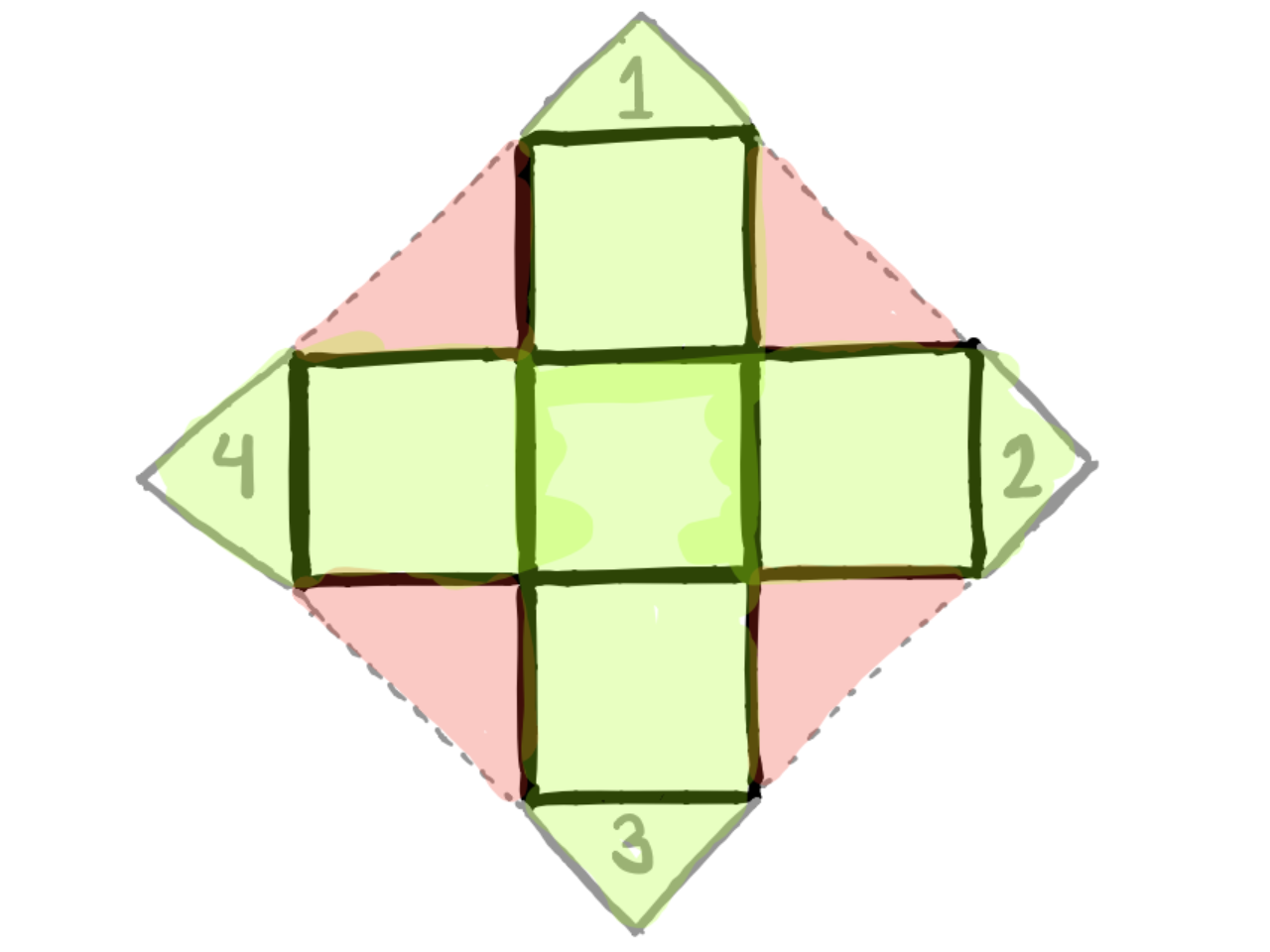
En comparaison avec l’image précédente, si on considère que le carré central (une face du cadeau) comme ayant une superficie de 1 unité carré (1u2), on a une surface totale de 1 unité carré (1u2) et on a 8 u2 perdues, avec une perte de 2 u2.
Il y a donc 2 observations intéressantes à faire ici :
- On utilise moins de papier en plaçant le cube en diagonale.
- On utilise une plus grande proportion du papier pour couvrir le cube (cadeau).
Si vous avez une méthode plus efficace que celle-là, s’il vous plait, faites-moi signe!
En attendant, je vais retourner mon rouleau de papier!
Après tout, c’est infiniment plus efficace d’utiliser une taie d’oreiller!