Netmath’s mission is to help every student discover and develop their own mathematical potential while having fun.
In this edition of “Simon is wondering…”, techno-pedagogue and Netmath expert Simon suggests that you tackle an everyday question from a mathematical perspective with your students. This approach will help them recognize that math can be really fun when it comes to better understanding the world around us.
Today, Simon is wondering why it’s important to be nice to your neighbour, and even what impact it can have on society in general. Here, our reflection will cover the concepts of calculating the area of a figure, representing a number, and constructing a possibility tree.
Being nice to your neighbour can apply to everyday, almost anecdotal, situations, like holding the door for the next person or giving up your seat to an elderly person on public transportation, but it also applies to more engaging situations, like sharing information.
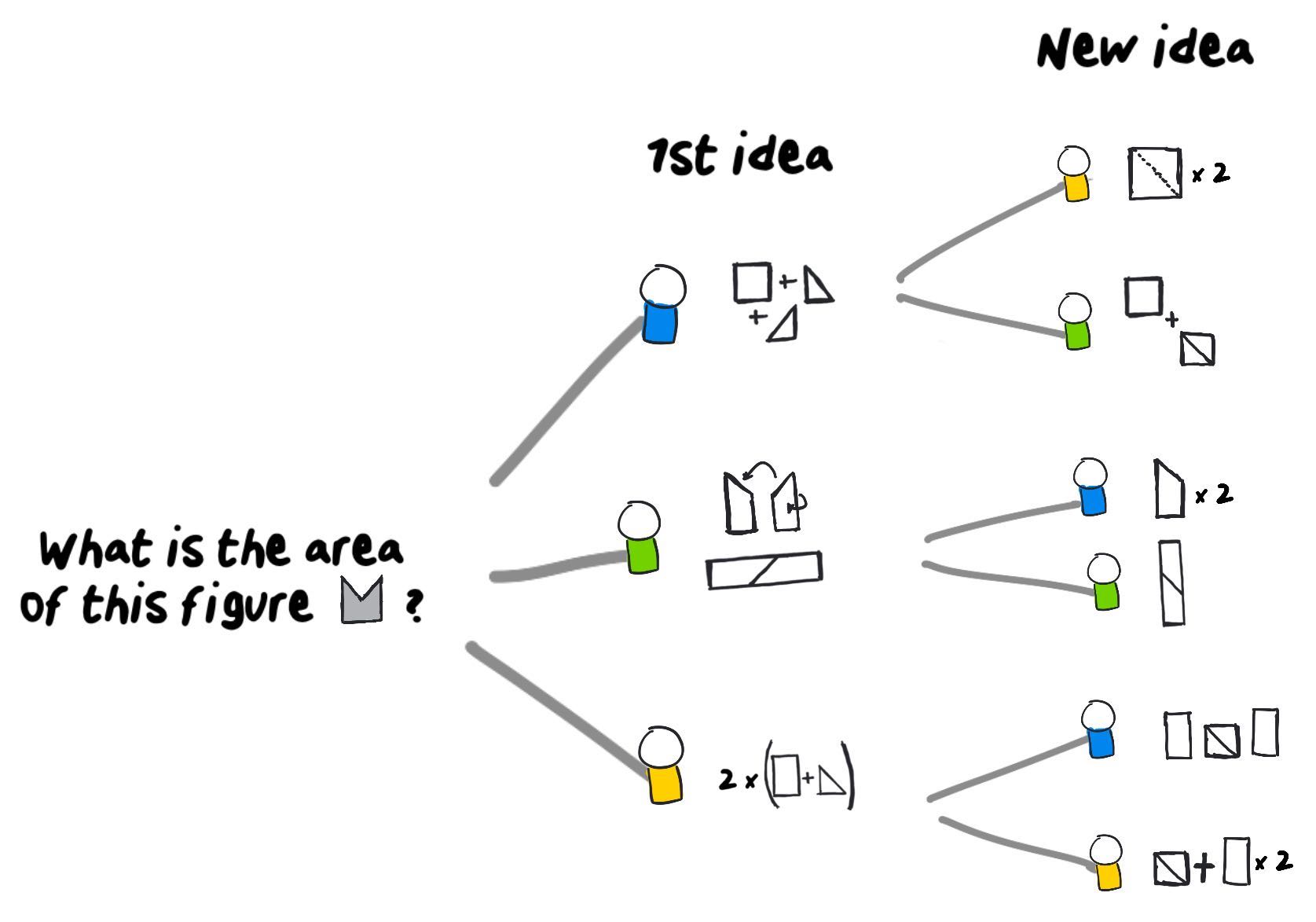
To understand what’s at stake here, I’m going to use a specific example. Let’s imagine that three students, Carl, Claire and Clarence, have to solve a math problem.
Here, we can see three excellent ways of arriving at the same result! However, Claire, Carl and Clarence each only have access to one solution… their own. That’s too bad, because as we can see from an outside perspective, each idea is different from the others. Each exploration has something special.
Now let’s imagine that they decide to think about the problem together. What happens?
At the end of their reflection, each student will have explored 3 different ways of solving the same math problem. To start with, I notice that the students have been exposed to 3 times more mathematical ideas: their own, plus those of the two other students, which adds up to 3 ideas.
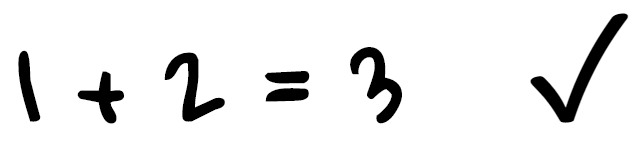
Everything works!
But I think it could go even further than this! One student could be inspired by the work of another!!!
OK. Imagine, for example, that all of the first ideas inspire the other students to come up with another idea! What would be the impact on the total number of mathematical explorations?
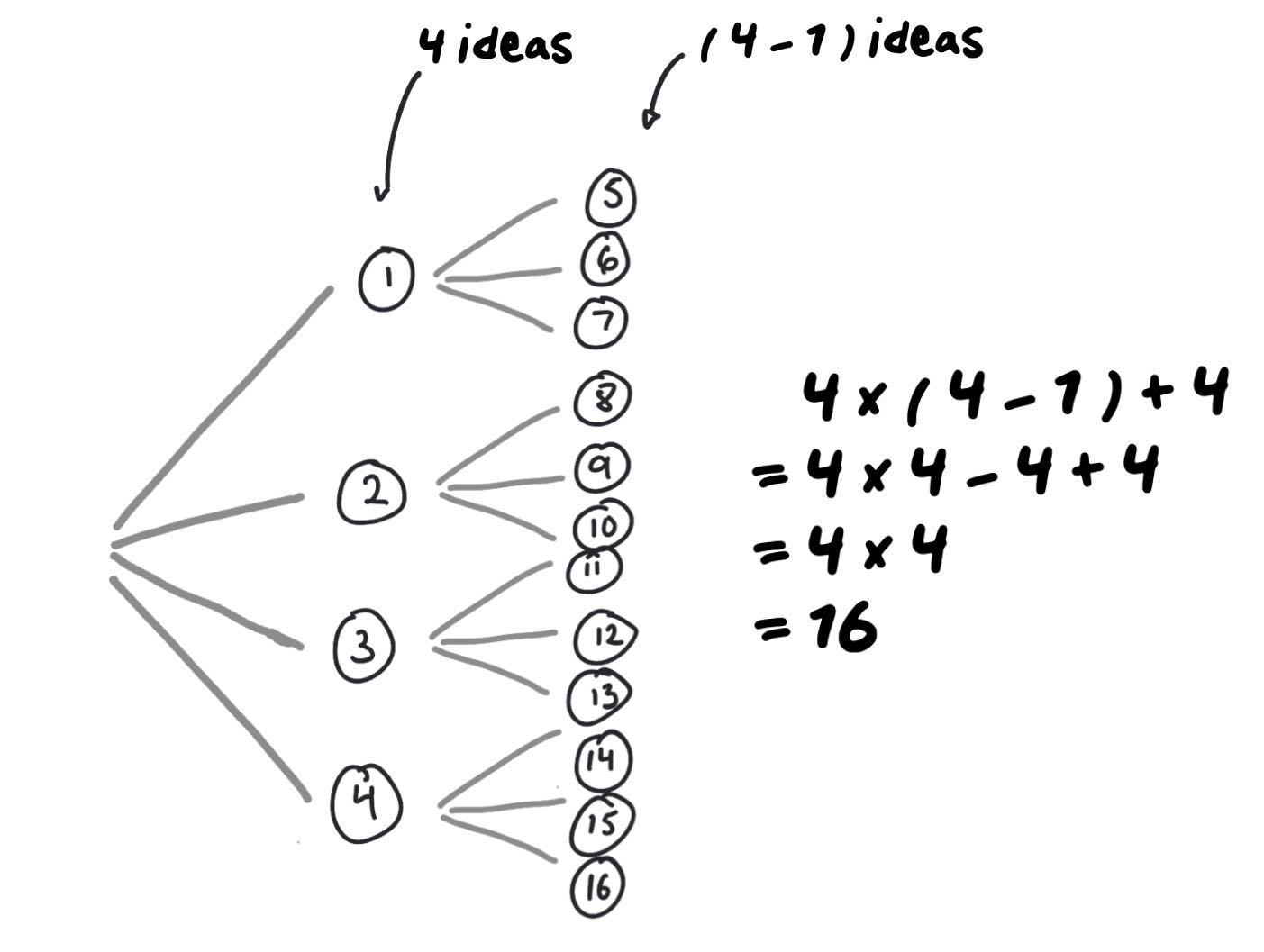
I think that the best way to answer this question is to make a possibility tree with all of the students’ ideas!
We can see that there are 3 ideas at the start, and these ideas inspire 6 new proposals… for a total of 3 + 6 = 9 solutions to the problem!
Interesting fact: 3 x 3 is also equal to 9! There were 3 students and we have a total of 9 ideas!
Does this mean that with 4 students, we would get 4 x 4 = 16 ideas?
It looks like that’s the case! We could even say that if there were n students, we’d end up with n x n ideas!
So for a class of 30 students, we would get… wow, 900 ideas!
It might seem scary for so many ideas to emerge, but trust collective intelligence. After the divergence phase, there is always a convergence phase, where the teacher has a key role to play!
In summary, being open to outside ideas allows us to look at situations in new ways. And like Jo Boaler, author of Mathematical Mindset, said, exposure to a variety of points of view enriches the quality of learning considerably. #growthmindset!
This year, we hope we’ll have the opportunity to share more of our ideas and learn from others.
So don’t forget to share this article and review these concepts in class with Netmath!