Understanding fractions clearly with Valérie Lebel, math resource teacher.

How to approach the understanding of fractions in class? Here is a simple idea that requires few resources but is extremely effective! Our Netmath expert, Simon Lavallée, recently discovered it thanks to Valérie Lebel, an Elementary math resource teacher at Dollard-Des-Ormeaux school of the Central Québec School Board. Now, he shares it with you!

Today, I will show you how the material used by Valérie can help your students to develop a conceptual understanding of what a fraction represents by varying what the whole represents. For each representation of the whole, the students must find to what ½, ⅓ and ¼ correspond.

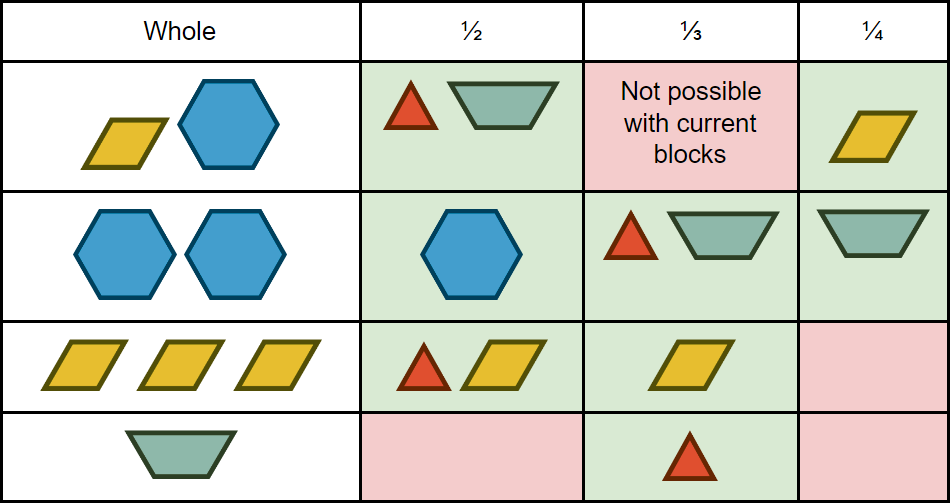
If you do not have the available material, you can print it here!

The boxes in red are impossible to reproduce using a single piece of material. It is a great opportunity to discuss in a large group the reasons behind this situation. Unfortunately, there is no piece that corresponds to these fractions (for example, 1/9 or 1/12). We can restart the debate by asking whether it is still possible to represent these fractions using blocks of patterns. Answer: There are endless ways to do so!

Valérie proposes another very interesting learning sequence to generate interest in class, particularly concerning equivalent fractions! For this, she uses bars.

Here’s how:

Step 1

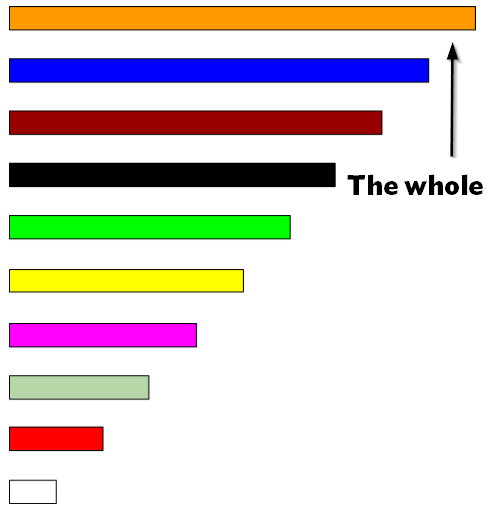
• We will take the orange bar to represent “the whole“
• Show me a 1/2? (Answer: 1 yellow bar, since 2 yellow bars form the whole)
• Show me 1/5? Answer: 1 red bar OR 2 white bars as they are equivalent fractions)
• What does the white bar represent? (Answer: 1/10)
• What do 2 red bars represent? (Answer: ⅖ , since 1 red bar represents ⅕, therefore 2 red bars represent ⅖ )
• What does 1 black bar represent? (Answer: 7/10)
• What do 4 red bars represent? (Answer: 4/5 or 8/10, because they are equivalent fractions)

Let your imagination run wild, or even better, challenge your students to ask a question to the class, you might be surprised!

Step 2

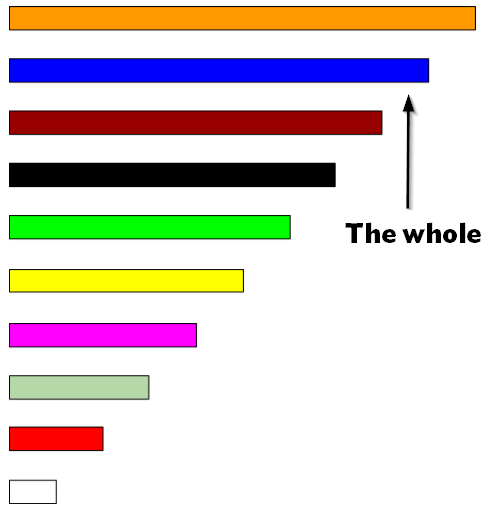
• We will take the blue bar to represent “the whole“
• Show me 1/2. (Answer: impossible with these bars)
• Show me 1/3. (Answer: 1 light gray bar since 3 gray bars form the whole.)
• Show me 2/3. (Answer: 2 light gray bars or …)
• What does 1 white bar represent? (Answer: 1/9)
• What does 1 black bar represent? (Answer: 7/9)

Step 3

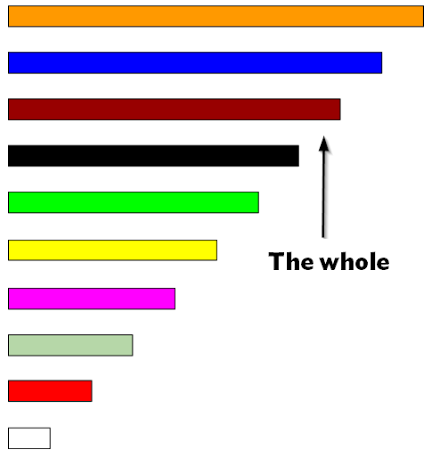
• We will take the brown bar to represent “the whole“
• Show me 1/2. (Answer: 1 pink bar, since two pink bars form a whole)
• Shown me 1/3. (Answer: impossible with these bars)
• Show me 1/4. (Answer: 1 red bar or …)
• What does a white bar represent? (Answer: 1/8)
• What does a black bar represent? (Answer: 7/8)

Each time students can use the bars to find more than one answer, which inevitably leads to discussions about the very nature of equivalent fractions. You could even carry on with fractional numbers. For example: in step 3, what do 3 or 5 or 8 pink bars represent? Ingenious, right? Next time, I will present another activity used by Valerie to help your students understand how the addition of fractions works.

If you too have a particular approach to tackle this mathematical concept, please don’t hesitate to share it in the comments section. In the meantime, I encourage you to explore representing fractions on Netmath whether in class or at home. To do so, here are 4 carefully selected activities to send to your students.